벤포드의 법칙
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
벤포드의 법칙은 숫자 집합에서 첫 번째 자릿수의 빈도가 1부터 9까지의 숫자에 대해 특정 확률 분포를 따른다는 경험적 법칙이다. 이 법칙은 1938년 프랭크 벤포드가 발견했으며, 자연적으로 발생하는 데이터에서 작은 숫자가 더 자주 나타나는 경향을 설명한다. 벤포드의 법칙은 회계 부정 탐지, 선거 부정 탐지 등 다양한 분야에 적용되며, 데이터가 여러 자릿수에 걸쳐 비교적 균일하게 분포할 때 정확도가 높다.
더 읽어볼만한 페이지
- 확률분포 이론 - 멱법칙
멱법칙은 형태로 표현되는 수학적 관계로, 척도 불변성을 가지며 자연 및 사회 현상을 설명하는 데 사용되고 통계적 완전성을 따르지 않는 특징을 가진다. - 통계 법칙 - 파레토 법칙
파레토 법칙은 소수의 원인이 대부분의 결과에 영향을 미친다는 경험적 법칙으로, 80/20 법칙으로 알려져 있으며, 다양한 분야에서 활용되지만, 단순화 및 인과관계 설명 부족 등의 비판도 존재한다. - 통계 법칙 - 멱법칙
멱법칙은 형태로 표현되는 수학적 관계로, 척도 불변성을 가지며 자연 및 사회 현상을 설명하는 데 사용되고 통계적 완전성을 따르지 않는 특징을 가진다. - 확률분포 - 베르누이 분포
베르누이 분포는 성공 확률 p를 가지며, 단 한 번의 시행에서 성공 또는 실패 두 가지 결과를 나타내는 이산 확률 분포로, 기댓값은 p, 분산은 p(1-p)이며 다른 여러 확률 분포와 관련되어 불확실성과 정보량을 측정할 수 있다. - 확률분포 - 로그 정규 분포
로그 정규 분포는 확률 변수 X의 로그가 정규 분포를 따르며, 양의 실수 값을 갖고 평균 μ와 표준 편차 σ를 매개변수로 갖는 확률 분포이다.
2. 정의
어떤 숫자 집합에서 첫째 자리 수 ()가 다음 확률 분포를 따를 때, 이 집합이 벤포드의 법칙을 따른다고 한다.[20]
:
이러한 집합의 선두 자릿수는 다음과 같은 분포를 가진다.
이 값은 로그 눈금에서 와 사이의 공간에 비례한다.
벤포드의 법칙은 십진법 외의 다른 기수에서도 성립하며, 일반적인 형태는 다음과 같다.[9]
:
보다 형식적으로 기술하면, 기저가 일 때 첫 번째 자릿수 의 출현 확률은 다음과 같다.
:
기저가 10인 경우(십진수), 벤포드의 법칙에 따르면 첫 번째 자릿수의 분포는 다음과 같다. (단, 는 첫 번째 자릿수, 는 확률)
어떤 숫자 집합에서 첫째 자리 숫자 ()가 다음 확률 분포를 따를 때, 이 집합이 벤포드의 법칙을 따른다고 한다.
3. 설명
:[20]
이 법칙에 따르면, 첫째 자리 숫자의 분포는 다음과 같다.
이는 숫자의 ''로그'' 값이 균등하고 무작위로 분포될 때 예상되는 분포이다. 예를 들어 1부터 10 사이의 숫자 x에서, x가 1 ≤ x < 2 이면 첫째 자리는 1이고, 9 ≤ x < 10 이면 첫째 자리는 9이다. log x의 관점에서 보면, [log 1, log 2] 구간이 [log 9, log 10] 구간보다 훨씬 넓기 때문에, log x가 균등 분포를 따르면 첫째 자리가 1일 확률이 9일 확률보다 더 높다.
벤포드의 법칙은 십진법 외의 다른 기수에도 적용된다. 일반적인 형태는 다음과 같다.[9]
:
(단, b는 2 이상의 정수)
벤포드의 법칙은 여러 자릿수에 걸쳐 있는 데이터에 가장 정확하게 적용된다. 예를 들어, 영국의 정착지 인구는 벤포드의 법칙을 따를 가능성이 높지만, 인구가 300~999명 사이인 마을로 정의하면 벤포드의 법칙이 적용되지 않을 수 있다.[13][14]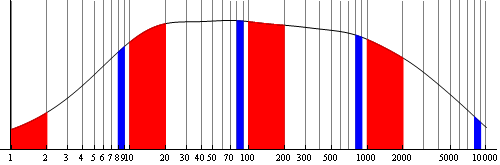
주가나 도시 인구처럼 여러 자릿수에 걸쳐 비교적 균일하게 분포하는 데이터는 벤포드의 법칙을 따를 가능성이 높다. 반면, IQ 점수나 성인 키처럼 한 자릿수에 몰려 있는 분포는 벤포드의 법칙을 따르지 않을 가능성이 높다.[13][14]
벤포드의 법칙은 곱셈 변동에서 비롯되는 경우가 많다.[22] 주가가 매일 0.99~1.01 사이의 무작위 요인으로 곱해지면, 시간이 지남에 따라 주가 분포는 벤포드의 법칙을 따른다. 이는 주가의 로그가 확률보행을 겪어 분포가 넓어지기 때문이다.[22] 반면 덧셈 변동은 정규 분포로 이어져 벤포드의 법칙을 만족하지 않는다.
안톤 포르만(Anton Formann)은 유효 숫자와 종속 변수 분포 사이의 상호 관련성을 통해 벤포드의 법칙을 설명했다. 그는 시뮬레이션 연구에서 확률 변수의 긴 오른쪽 꼬리 분포가 뉴컴-벤포드의 법칙과 일치하며, 두 확률 변수의 비율 분포에서 적합성이 향상됨을 보였다.[23] IQ 점수나 인간 신장처럼 정규 분포를 따르는 변수는 벤포드의 법칙을 만족하지 않지만,[24] 이러한 분포에서 숫자를 "혼합"하면 벤포드의 법칙이 다시 나타난다.[25][26]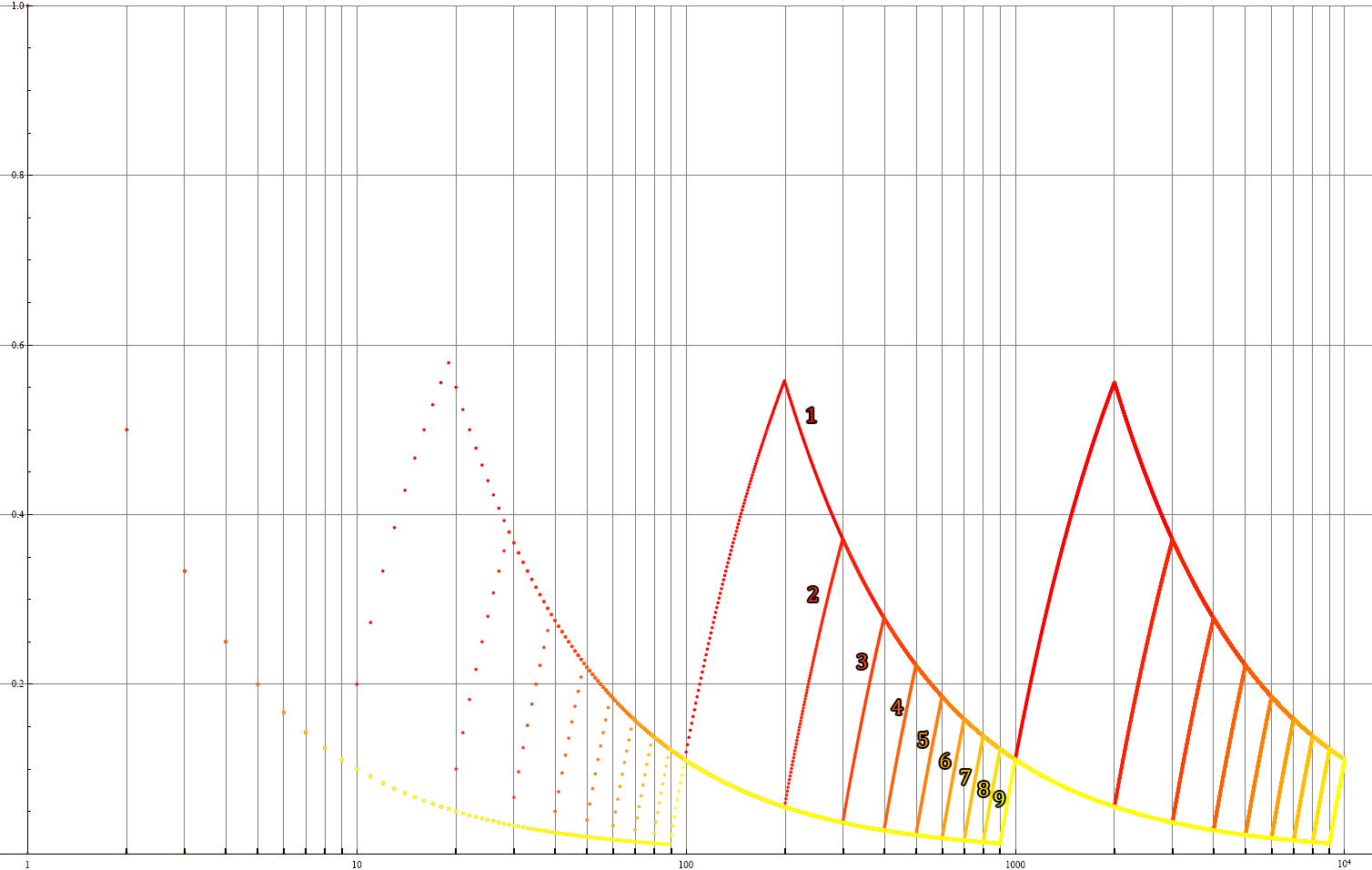
3. 1. 로그 스케일에서의 분포 폭
어떤 숫자 집합의 첫째 자릿수 d (d ∈ {1, ..., 9})가 다음 확률로 나타나면, 이 집합은 벤포드의 법칙을 만족한다고 한다.[20]
: P(d) = log10(d + 1) - log10(d) = log10((d + 1)/d) = log10(1 + 1/d).
이러한 집합의 첫째 자릿수는 다음과 같은 분포를 가진다.
P(d)는 로그 눈금에서 d와 d + 1 사이의 공간에 비례한다. 그러므로 이것은 숫자가 아니라, 숫자의 로그가 균등하고 무작위로 분포될 경우 예상되는 분포이다.
예를 들어, 1과 10 사이에 있도록 제한된 숫자 x는 1 ≤ x < 2이면 숫자 1로 시작하고, 9 ≤ x < 10이면 숫자 9로 시작한다. 따라서, x는 log 1 ≤ log x < log 2이면 숫자 1로 시작하고, log 9 ≤ log x < log 10이면 9로 시작한다. 구간 [log 1, log 2]는 구간 [log 9, log 10]보다 훨씬 넓다(각각 0.30과 0.05). 그러므로 만약 log x가 균등하고 무작위로 분포되어 있다면, 더 넓은 구간에 속할 가능성이 더 좁은 구간에 속할 가능성보다 훨씬 높다. 즉, 9보다 1로 시작할 가능성이 더 높으며, 확률은 구간 너비에 비례하며, 위 식을 제공한다.
보다 형식적으로 기술하면, 밑이 b (b ≥ 2)일 때 첫째 자릿수 d (d ∈ {1, …, b - 1})의 출현 확률은, P(d) = logb (d + 1) - logb d = logb ((d + 1)/d)라는 식을 따른다. 이 값은 엄밀히 로그 스케일에서 d와 d + 1 사이의 공간과 같다.
밑이 10인 경우 (십진수), 벤포드의 법칙에 따르면 첫째 자릿수의 분포는 다음과 같다. (d는 첫째 자릿수, p는 확률)
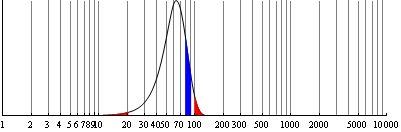
위에 제시된 두 그림은 로그 스케일에 나타낸 두 개의 확률 분포이다.[76] 두 그림 모두, 빨간색으로 표시된 부분의 면적이 첫째 자리가 1일 확률에 비례하고, 파란색으로 표시된 부분의 면적이 첫째 자리가 8일 확률에 비례한다.
왼쪽 분포에서는 빨간색과 파란색 영역의 면적비가 대략 각 폭의 비와 같아진다. 폭의 비는 보편적이며, 벤포드의 법칙에 의해 엄밀하게 주어진다. 따라서 이러한 확률 분포를 따르는 수치는 대개 벤포드의 법칙을 따른다.
반면, 오른쪽 분포에서는 빨간색과 파란색 영역의 면적비가 그 폭의 비에서 크게 벗어난다. 오른쪽 그림에서도 폭의 비는 왼쪽 분포와 동일하다. 빨간색과 파란색 영역의 면적비는 그 폭보다는 오히려 높이의 비에 의존하여 결정된다. 폭과 달리 높이는 벤포드의 법칙에 보편적인 관계를 만족시키지 않는다. 대신 그 수치의 분포 형태에 의해 완전히 결정된다. 따라서 첫째 자릿수의 분포는 벤포드의 법칙을 전혀 만족시키지 않는다.
보다 일반적으로, 소득의 분포나 시/군/구의 인구 분포 등, 여러 자릿수의 범위에서 상당히 부드럽게 퍼져 있는 분포는 위 왼쪽 그림처럼 벤포드의 법칙을 잘 만족시킨다. 반면, 성인의 신장이나 IQ 수치 등 1자리 또는 2자리의 범위에서만 분포하는 것은 위 오른쪽 그림처럼 벤포드의 법칙을 잘 만족시키지 않는다.[77]
3. 2. 지수적 성장 과정
벤포드의 법칙은 여러 자릿수에 걸쳐있는 데이터에 가장 정확하게 적용되는 경향이 있다. 데이터가 더 많은 자릿수를 균등하게 포함할수록 벤포드의 법칙은 더 정확하게 적용된다. 예를 들어, 영국의 정착지 인구를 나타내는 숫자 목록에는 벤포드의 법칙이 적용될 것으로 예상할 수 있지만, "정착지"가 인구 300명에서 999명 사이의 마을로 정의된다면 적용되지 않는다.[13][14]로그 스케일에서 확률 분포를 살펴보면, 넓은 분포에서는 첫 번째 숫자가 1일 확률(빨간색 면적)이 8일 확률(파란색 면적)보다 크므로 벤포드의 법칙을 따르지만, 좁은 분포에서는 그렇지 않다.[14]
따라서 주식 시장 가격이나 도시 인구처럼 여러 자릿수에 걸쳐 비교적 균일하게 분포하는 실제 데이터는 벤포드의 법칙을 따를 가능성이 높다. 반면, IQ 점수나 성인 키처럼 대부분 한 자릿수에 몰려 있는 분포는 벤포드의 법칙을 따르지 않을 가능성이 높다.[13][14]
벤포드의 법칙의 실제 사례는 곱셈 변동에서 비롯된다.[22] 예를 들어, 주가가 매일 0.99에서 1.01 사이의 무작위 요인으로 곱해지면, 오랜 기간 동안 주가 확률 분포는 벤포드의 법칙을 만족한다. 이는 주가의 ''로그''가 확률보행을 겪어 시간이 지남에 따라 분포가 넓고 매끄러워지기 때문이다.[22] 중심 극한 정리에 따르면, 많은 확률 변수를 곱하면 분산이 커지는 로그 정규 분포가 생성되어 결국 여러 자릿수를 균일하게 덮게 된다.
반면 덧셈 변동은 정규 분포로 이어져 벤포드의 법칙을 만족하지 않는다. 가상의 주가는 많은 확률 변수의 ''곱''으로 표현될 수 있으므로 벤포드의 법칙을 따를 가능성이 있다.
피보나치 수,[59][60] 계승,[61] 2의 거듭제곱[62][63] 등 잘 알려진 무한 정수 수열과 지수 성장 또는 지수 감소 과정은 정확히 벤포드의 법칙을 만족하는 것으로 증명되었다.
어떤 양이 지수적으로 증가하거나 감소하면, 각 첫 번째 자릿수를 갖는 시간의 백분율은 점근적으로 벤포드의 법칙을 만족한다. 예를 들어, 어떤 양이 1년마다 2배가 된다고 가정하면, 첫 번째 자릿수는 1년 차에는 1, 2년 차에는 2와 3, 3년 차에는 4, 5, 6, 7, 4년 차에는 8과 9를 거쳐 다시 1로 돌아온다. 이처럼 지수적으로 증가하는 값은 벤포드의 법칙을 따른다.
3. 3. 스케일 불변성
어떤 숫자 집합의 첫 자릿수 (d)가 다음 확률로 나타나면, 이 집합은 벤포드의 법칙을 만족한다고 한다.[20]:
이러한 집합의 선두 자릿수는 다음과 같은 분포를 가진다.
값은 로그 눈금에서 와 사이의 공간에 비례한다. 그러므로 이것은 숫자가 아니라, 숫자의 ''로그''가 균등하고 무작위로 분포될 경우 예상되는 분포이다.
벤포드의 법칙은 때때로 더 강력한 형태로 언급되는데, 데이터의 로그의 소수 부분이 일반적으로 0과 1 사이에서 균등하게 분포된다고 주장하며, 이를 통해 첫 번째 자릿수의 분포에 대한 주요 주장을 도출할 수 있다.[5]
벤포드의 법칙을 확장하면 십진법 외의 다른 기수에서 첫 번째 숫자의 분포를 예측할 수 있다. 실제로 b ≥ 2 인 모든 기수에서 성립한다. 일반적인 형태는 다음과 같다.[9]
:
b = 1, 2 ( 일진법, 이진법) 숫자 체계의 경우 벤포드의 법칙은 참이지만 자명하다. 모든 이진수와 일진수(0 또는 공집합 제외)는 숫자 1로 시작한다.
데이터 집합의 첫 번째 숫자 분포가 스케일 불변성(데이터가 표현되는 단위와 무관)일 때, 항상 벤포드의 법칙에 의해 주어진다.[28][29]
예를 들어, 길이 목록의 첫 번째 (영이 아닌) 숫자는 측정 단위가 피트 또는 야드인지에 관계없이 동일한 분포를 가져야 한다. 1 야드는 3 피트이므로, 야드 단위 길이의 첫 번째 숫자가 1일 확률은 피트 단위 길이의 첫 번째 숫자가 3, 4 또는 5일 확률과 같아야 한다. 마찬가지로, 야드 단위 길이의 첫 번째 숫자가 2일 확률은 피트 단위 길이의 첫 번째 숫자가 6, 7 또는 8일 확률과 같아야 한다. 이를 모든 가능한 측정 규모에 적용하면 벤포드의 법칙의 로그 분포가 된다.
첫 번째 숫자에 대한 벤포드의 법칙은 숫자 체계에 대해 기수 불변이다.
만약 실제로 첫 번째 자릿수의 숫자가 특정 분포를 보인다면, 측정 단위를 변경하더라도 마찬가지로 특정 분포를 나타내야 한다. 예를 들어, 길이 측정값을 피트에서 야드로 상수를 곱하여 변경하더라도 분포는 불변해야 한다. 이것은 스케일 불변성이며, 이러한 조건을 만족하는 유일한 분포가 로그 분포이다.
어떤 물체의 길이 또는 거리 등의 첫 번째 자릿수 (0 제외)는, 측정 단위가 피트나 야드 또는 다른 무엇이든, 동일한 분포를 가져야 한다. 1 야드는 3 피트이므로, 야드로 측정된 길이의 첫 번째 자릿수가 1일 확률은, 피트로 측정된 길이의 첫 번째 자릿수가 3, 4, 5 중 하나일 확률과 같아야 한다. 이를 모든 측정 단위에 대해 동일하게 생각하면 로그 분포가 되며, log10(1) = 0과 log10(10) = 1임을 고려하면 벤포드의 법칙이 된다. 즉, 첫 번째 자릿수에 특정 분포가 있다면, 이는 어떤 측정 단위가 사용되든 적용될 수 있어야 하며, 그러한 조건에 적합한 유일한 첫 번째 자릿수 분포가 벤포드의 법칙이다.
3. 4. 다중 확률 분포
어떤 집합에 속한 수들의 첫째 자리 ()가 다음의 확률 분포를 따를 때, 이 집합이 벤포드의 법칙을 따른다고 한다.:[20]
이러한 집합의 선두 자릿수는 다음과 같은 분포를 가진다.
위 표에서 수량 는 로그 눈금에서 와 사이의 공간에 비례한다. 그러므로 이것은 숫자가 아니라, 숫자의 ''로그''가 균등하고 무작위로 분포될 경우 예상되는 분포이다.
예를 들어, 1과 10 사이에 있도록 제한된 숫자 는 이면 숫자 1로 시작하고, 이면 숫자 9로 시작한다. 따라서, 는 이면 숫자 1로 시작하고, 이면 9로 시작한다. 구간 는 구간 보다 훨씬 넓다(각각 0.30과 0.05). 그러므로 만약 가 균등하고 무작위로 분포되어 있다면, 더 넓은 구간에 속할 가능성이 더 좁은 구간에 속할 가능성보다 훨씬 높다. 즉, 9보다 1로 시작할 가능성이 더 높으며, 확률은 구간 너비에 비례하며, 위 식을 제공한다.
벤포드의 법칙은 때때로 데이터의 로그의 소수 부분이 일반적으로 0과 1 사이에서 균등하게 분포된다고 주장하며, 이를 통해 첫 번째 자릿수의 분포에 대한 주요 주장을 도출할 수 있다.[5]
벤포드의 법칙은 여러 자릿수에 걸쳐있는 데이터에 가장 정확하게 적용되는 경향이 있다. 일반적으로, 데이터가 더 많은 자릿수를 균등하게 포함할수록 벤포드의 법칙은 더 정확하게 적용된다. 예를 들어, 벤포드의 법칙은 영국의 정착지 인구를 나타내는 숫자 목록에 적용될 것으로 예상할 수 있다. 하지만 "정착지"가 인구 300명에서 999명 사이의 마을로 정의된다면, 벤포드의 법칙은 적용되지 않을 것이다.[13][14]
따라서 여러 자릿수에 걸쳐 비교적 균일하게 분포하는 실제 데이터 (예: 주식 시장 가격 및 마을, 읍, 도시의 인구)는 벤포드의 법칙을 매우 정확하게 만족시킬 가능성이 높다. 반면에, 대부분 또는 전체가 한 자릿수 내에 있는 분포 (예: IQ 점수 또는 성인 인간의 키)는 벤포드의 법칙을 매우 정확하게, 혹은 전혀 만족시키지 못할 가능성이 높다.[13][14] 그러나 적용 가능한 범위와 적용 불가능한 범위 간의 차이는 날카로운 경계가 아니다. 분포가 좁아질수록 벤포드의 법칙에서 벗어나는 정도가 점차 증가한다.
벤포드의 법칙의 많은 실제 사례는 곱셈 변동에서 비롯된다.[22] 예를 들어, 주가가 100달러에서 시작하여 매일 0.99에서 1.01 사이의 무작위로 선택된 요인으로 곱해진다면, 오랜 기간 동안 주가 확률 분포는 점점 더 높은 정확도로 벤포드의 법칙을 만족한다.
그 이유는 주가의 ''로그''가 확률보행을 겪고 있기 때문에 시간이 지남에 따라 확률 분포가 점점 더 넓고 매끄러워지기 때문이다.[22] (더 기술적으로 말하면, 중심 극한 정리는 점점 더 많은 확률 변수를 곱하면 분산이 커지는 로그 정규 분포가 생성되므로 결국 거의 균일하게 여러 자릿수를 커버한다고 말한다.)
곱셈 변동과 달리 ''덧셈'' 변동은 벤포드의 법칙으로 이어지지 않는다. 대신 정규 분포로 이어진다 (다시 중심 극한 정리에 의해). 이는 벤포드의 법칙을 만족하지 않는다. 반대로 위에 설명된 가상의 주가는 많은 확률 변수의 ''곱'' (즉, 각 날짜의 가격 변동 요인)으로 쓸 수 있으므로 벤포드의 법칙을 상당히 잘 따를 ''가능성''이 있다.
안톤 포르만(Anton Formann)은 유효 숫자의 확률 분포와 종속 변수의 분포 사이의 상호 관련성에 주목함으로써 다른 설명을 제시했다. 그는 시뮬레이션 연구에서 확률 변수의 긴 오른쪽 꼬리 분포가 뉴컴-벤포드의 법칙과 일치하며, 두 확률 변수의 비율 분포의 경우 적합성이 일반적으로 향상된다는 것을 보여주었다.[23] 특정 분포 (IQ 점수, 인간 신장)에서 추출된 숫자의 경우 벤포드의 법칙이 적용되지 않는데, 이러한 변량은 벤포드의 법칙을 만족하지 않는 것으로 알려진 정규 분포를 따르기 때문이다.[24] 정규 분포는 여러 자릿수를 포괄할 수 없으며, 로그의 가수가 (대략적으로라도) 균일하게 분포하지 않기 때문이다. 그러나 이러한 분포에서 숫자를 "혼합"하면, 예를 들어 신문 기사에서 숫자를 가져오면 벤포드의 법칙이 다시 나타난다. 이것은 수학적으로도 증명할 수 있다. 즉, (상관 관계가 없는 집합에서) 반복적으로 확률 분포를 "무작위로" 선택한 다음 해당 분포에 따라 숫자를 무작위로 선택하면 결과 숫자 목록이 벤포드의 법칙을 따른다.[25][26]
4. 적용과 제한
벤포드의 법칙은 다양한 분야에 적용되지만, 특정한 경우에는 적용되지 않거나 제한될 수 있다.
적용 사례:
- 회계 부정 탐지: 1972년 할 배리언은 공공 계획 결정 지원을 위해 제출된 사회 경제 데이터에서 조작된 수치를 탐지하는 데 벤포드의 법칙을 사용할 수 있다고 제안했다. 숫자를 조작하는 사람들은 숫자를 비교적 균등하게 분포시키는 경향이 있으므로, 데이터의 첫 번째 숫자 빈도 분포와 벤포드의 법칙에 따른 예상 분포를 비교하면 이상한 결과를 발견할 수 있다.[32]
- 선거 부정 탐지: 월터 메베인은 선거 분석에 두 번째 자릿수 벤포드의 법칙 검사(2BL-test)를 처음으로 적용했다.[34] 그러나 벤포드의 법칙을 선거에 적용하는 것에 대한 과학적 합의는 이루어지지 않았다.[35][36][37]
- 기타:
- 미국에서는 벤포드의 법칙에 근거한 증거가 형사 사건에서 증거로 채택되기도 했다.[33]
- 유로존 가입 전 그리스 정부가 유럽 연합에 보고한 거시 경제 데이터가 벤포드의 법칙에 따라 사기일 가능성이 제기되었다.[47][48]
- 오픈 리딩 프레임 수와 게놈 크기의 관계, 출판된 논문의 회귀 계수, 슬로베니아 과학자들의 논문 수 등 다양한 연구에서 벤포드의 법칙이 확인되었다.[50][51][52]
제한:
- 데이터 범위: 벤포드의 법칙은 여러 자릿수에 걸쳐 있는 데이터에 가장 잘 적용된다. 데이터 범위가 좁으면 법칙이 적용되지 않을 수 있다. 예를 들어, 특정 인구 범위로 제한된 마을 인구는 벤포드의 법칙을 따르지 않을 수 있다.[13][14]
- 분포 형태: 실제 데이터는 종류에 따라 수치 분포 방식이 왜곡되어 벤포드의 법칙을 만족하지 않는 경우가 있다.
- 특정 값 배제: 특정 값이 정의에 의해 배제되는 경우 (예: 인구 300~999명의 마을) 벤포드의 법칙을 적용할 수 없다.
- 벤포드의 법칙을 따를 것으로 예상되는 분포:
- 평균이 중앙값보다 크고 왜도가 양수인 경우
- 수의 수학적 결합 (예: 수량 × 가격)
- 거래 수준 데이터 (예: 지출, 판매)
- 벤포드의 법칙을 따르지 않을 것으로 예상되는 분포:
- 순차적으로 할당된 숫자 (예: 수표 번호)
- 인간의 사고에 영향을 받는 숫자 (예: 심리적 임계값으로 설정된 가격)
- 회사별 숫자가 많은 계정
- 내장된 최소 또는 최대값을 가진 계정
- 수의 차수가 범위를 벗어나는 분포
- 기타: 연속된 자연수의 제곱근과 역수,[64] 유한 범위 내의 소수,[65] 지역 전화번호 목록,[66] 특정 인구 범위로 제한된 지역의 인구,[64] 병리 보고서의 마지막 숫자[67] 등은 벤포드의 법칙을 따르지 않거나 위반한다.
4. 1. 회계 부정 탐지
1972년, 할 배리언은 공공 계획 결정 지원을 위해 제출된 사회 경제 데이터 목록에서 숫자를 허위로 조작하는 경우, 숫자를 비교적 균등하게 분포시키는 경향이 있다는 점을 이용하여 부정을 탐지할 수 있다고 제안했다. 데이터에서 첫 번째 숫자의 빈도 분포와 벤포드의 법칙에 따른 예상 분포를 비교하면 이상한 결과를 나타낼 수 있다.[32] 이 아이디어를 바탕으로 마크 니그리니(Mark Nigrini)는 벤포드의 법칙이 회계 및 지출 관련 사기의 지표로 사용될 수 있음을 보여주었다.[81]4. 2. 선거 부정 탐지
월터 메베인(Walter Mebane) 미시간 대학교 정치학자이자 통계학자는 두 번째 자릿수 벤포드의 법칙 검사(2BL-test)를 선거 분석(election forensics)에 처음으로 적용했다.[34] 이러한 분석은 선거 결과의 부정을 식별하는 간단하지만, 완벽하지는 않은 방법으로 간주된다.[35] 그러나, 문헌에서는 벤포드의 법칙을 선거에 적용하는 것을 뒷받침하는 과학적 합의가 이루어지지 않았다. 2011년 정치학자 조셉 데커트, 미하일 미야고프, 그리고 피터 C. 오데스훅(Peter C. Ordeshook)의 연구는 벤포드의 법칙이 선거 부정의 통계적 지표로 문제적이고 오해의 소지가 있다고 주장했다.[36] 그들의 방법론은 메베인에 의해 반박되었지만, 그는 벤포드의 법칙을 선거 데이터에 적용하는 데 많은 주의사항이 있다는 데 동의했다.[37]벤포드의 법칙은 2009년 이란 선거에서 부정의 증거(Results of the 2009 Iranian presidential election#Initial Digit Distribution/Benford's Law)로 사용되었다.[38] 메베인의 분석에 따르면, 선거에서 승리한 마무드 아마디네자드(Mahmoud Ahmadinejad) 대통령의 득표수에서 두 번째 자릿수는 벤포드의 법칙의 기대치와 크게 달랐고, 무효표(invalid vote)가 거의 없는 투표함이 결과에 더 큰 영향을 미쳐 광범위한 투표 조작(ballot stuffing)을 시사했다.[39] 또 다른 연구에서는 부트스트랩 (통계학)(bootstrapping (statistics)) 시뮬레이션을 사용하여 후보 메흐디 카루비(Mehdi Karroubi)가 벤포드의 법칙에 따라 예상되는 것보다 거의 두 배나 많은 7로 시작하는 득표수를 얻었다는 것을 발견했으며,[40] 컬럼비아 대학교(Columbia University)의 분석에서는 공정한 선거에서 2009년 이란 대통령 선거에서 발견된 인접하지 않은 자릿수가 너무 적고 마지막 자릿수 빈도에서 의심스러운 편차가 나타날 확률이 0.5% 미만이라고 결론지었다.[41] 벤포드의 법칙은 또한 2003년 캘리포니아 주지사 선거(2003 California gubernatorial election),[42] 2000년 미국 대통령 선거(United States presidential election, 2000)와 2004년 미국 대통령 선거(2004 United States presidential election)[43] 및 2009년 독일 연방 선거(2009 German federal election)의 데이터에 대한 사법 감사 및 부정 탐지에 적용되었으며,[44] 벤포드의 법칙 검사는 "부정에 대한 통계적 검사로 심각하게 고려할 가치가 있다"고 밝혀졌지만 "우리가 알고 있는 많은 표에 유의미하게 영향을 미치는 왜곡에 민감하지 않다"고 밝혀졌다.
벤포드의 법칙은 또한 선거 부정을 주장하는 데 잘못 적용되기도 했다. 조 바이든(Joe Biden)의 2020년 미국 대통령 선거(2020 United States presidential election) 시카고(Chicago), 밀워키(Milwaukee) 및 기타 지역의 선거 결과에 법칙을 적용했을 때, 첫 번째 자릿수의 분포는 벤포드의 법칙을 따르지 않았다. 이러한 오적용은 데이터 범위가 좁은 데이터를 살펴보는 결과였는데, 이는 데이터 범위가 넓어야 한다는 벤포드의 법칙의 내재된 가정을 위반하는 것이다. 첫 번째 자릿수 검사는 구역별 데이터에 적용되었지만, 구역은 수천 표를 넘게 받거나 수십 표 미만으로 받는 경우가 드물기 때문에 벤포드의 법칙이 적용될 것으로 기대할 수 없다. 메베인에 따르면 "구역별 득표수의 첫 번째 자릿수는 선거 부정을 진단하는 데 유용하지 않다는 것이 널리 이해되고 있다."[45][46]
4. 3. 기타 응용
미국에서는 벤포드의 법칙에 근거한 증거가 연방, 주, 지방 정부 차원의 형사 사건에서 증거로 채택되어 왔다.[33] 유로존 가입 전 그리스 정부가 유럽 연합에 보고한 거시 경제 데이터는 벤포드의 법칙을 통해 사기일 가능성이 있는 것으로 나타났지만, 이는 그리스가 유로존에 가입한 지 여러 해가 지난 후였다.[47][48]
2002년 유로화 도입 전후 유럽 전역의 소비재 가격 연구에서, 연구자들은 심리적 가격 책정 패턴을 감지하기 위해 벤포드의 법칙을 사용했다.[49] 심리적 가격 책정이 없다면 품목 가격의 첫 번째, 두 번째, 세 번째 숫자가 벤포드의 법칙을 따라야 했고, 숫자의 분포가 벤포드의 법칙에서 벗어나는 경우(예: 9가 많은 경우)는 상인들이 심리적 가격 책정을 사용했을 수 있음을 의미했다.
2002년 유로화가 현지 통화를 대체했을 때, 짧은 기간 동안 유로화 상품 가격은 대체 전 현지 통화 상품 가격에서 간단히 환산되었다. 유로화 가격과 현지 통화 가격 모두에서 동시에 심리적 가격 책정을 하는 것은 본질적으로 불가능하기에, 전환 기간 동안 심리적 가격 책정은 이전부터 존재했더라도 중단되었을 것이고, 이는 소비자들이 단일 통화(유로)의 가격에 다시 익숙해진 후에만 재개될 수 있었다.
연구자들의 예상대로, 첫 번째 가격 숫자의 분포는 벤포드의 법칙을 따랐지만, 두 번째와 세 번째 숫자의 분포는 도입 전에 벤포드의 법칙에서 크게 벗어났고, 도입 기간에는 덜 벗어났으며, 도입 후에는 다시 더 벗어났다.
오픈 리딩 프레임 수와 게놈 크기의 관계는 진핵생물과 원핵생물 간에 차이를 보이는데, 전자는 로그 선형 관계를, 후자는 선형 관계를 보인다. 벤포드의 법칙은 두 경우 모두 데이터에 대한 훌륭한 적합성을 보여 이 관찰을 검증하는 데 사용되었다.[50]
출판된 논문의 회귀 계수에 대한 검사 결과는 벤포드의 법칙과 일치했다.[51] 비교를 위해 연구 대상자들에게 통계 추정치를 조작하도록 요청했는데, 조작된 결과는 첫 번째 자릿수에서는 벤포드의 법칙을 따랐지만, 두 번째 자릿수에서는 벤포드의 법칙을 따르지 못했다.
슬로베니아 국가 데이터베이스에 등록된 모든 연구자의 출판된 과학 논문 수를 테스트한 결과, 벤포드의 법칙을 강력하게 따르는 것으로 나타났다.[52] 또한, 저자들을 과학 분야별로 분류하여 테스트한 결과, 자연과학이 사회과학보다 더 큰 적합성을 보였다.
1972년, 할 배리언(Hal Varian)은 공공 계획 결정을 지원하기 위해 제출된 사회 경제적 데이터 목록에 포함된 조작된 값을 발견하기 위해 이 법칙을 사용할 수 있다고 시사했다. 데이터를 조작하는 사람은 해당 수치를 상당히 보편적으로 분포시키려고 할 것이라는 합리적인 가정을 바탕으로, 해당 데이터의 첫 번째 자릿수 분포 확률을 벤포드의 법칙에 따른 기대 분포 확률과 단순 비교함으로써 이상한 결과를 나타낼 수 있다.[80] 이 아이디어를 바탕으로 마크 니그리니(Mark Nigrini)는 벤포드의 법칙이 회계 및 지출 관련 사기의 지표로 사용될 수 있음을 보여주었다.[81]
4. 4. 제한
벤포드의 법칙은 여러 자릿수에 걸쳐있는 데이터에 가장 정확하게 적용되는 경향이 있다. 일반적으로 데이터가 더 많은 자릿수를 균등하게 포함할수록 벤포드의 법칙은 더 정확하게 적용된다. 예를 들어, 영국의 정착지 인구를 나타내는 숫자 목록에는 벤포드의 법칙이 적용될 것으로 예상할 수 있다. 하지만 "정착지"가 인구 300명에서 999명 사이의 마을로 정의된다면, 벤포드의 법칙은 적용되지 않는다.[13][14]아래의 로그 스케일로 표시된 확률 분포를 보면, 빨간색의 총 면적은 첫 번째 숫자가 1일 상대적 확률이고, 파란색의 총 면적은 첫 번째 숫자가 8일 상대적 확률이다. 첫 번째 분포의 경우, 빨간색과 파란색 면적 크기는 각 막대의 너비에 대략적으로 비례한다. 따라서 이 분포에서 추출된 숫자는 대략 벤포드의 법칙을 따른다. 반면에, 두 번째 분포의 경우, 빨간색과 파란색 면적 비율은 각 막대의 너비 비율과 매우 다르다. 빨간색과 파란색의 상대 면적은 너비보다 막대의 높이에 의해 더 많이 결정된다. 따라서 이 분포의 첫 번째 숫자는 벤포드의 법칙을 전혀 만족시키지 못한다.[14]
따라서 여러 자릿수에 걸쳐 비교적 균일하게 분포하는 실제 데이터 (예: 주식 시장 가격 및 마을, 읍, 도시의 인구)는 벤포드의 법칙을 매우 정확하게 만족시킬 가능성이 높다. 반면에, 대부분 또는 전체가 한 자릿수 내에 있는 분포 (예: IQ 점수 또는 성인 인간의 키)는 벤포드의 법칙을 매우 정확하게, 혹은 전혀 만족시키지 못할 가능성이 높다.[13][14] 그러나 적용 가능한 범위와 적용 불가능한 범위 간의 차이는 날카로운 경계가 아니다. 분포가 좁아질수록 벤포드의 법칙에서 벗어나는 정도가 점차 증가한다.
실사회 데이터는 그 데이터의 종류에 따라 수치 분포 방식이 왜곡되어 있는 경우가 있으며, 그 정도에 따라 벤포드의 법칙을 만족하지 않는 경우가 있다.
예를 들어, "이름이 'A'로 시작하는 영국의 마을 인구"나 "소액의 보험금 청구" 등은 벤포드의 법칙을 따를 것이라고 기대할 수 있다. 그러나 영국에서의 마을 정의가 "인구가 300명에서 999명까지의 집락"이라는 점이나, 소액의 보험금 청구의 정의가 "50달러에서 100달러까지의 청구"라는 것을 알게 되면, 특정 값이 정의에 의해 배제되어 벤포드의 법칙을 (단순하게는) 적용할 수 없다는 것을 알 수 있다.
이진 표현에서는 이 현상의 가장 극단적인 예가 나타난다. 일반적인 표기 방법, 즉 이른바 "선행 0"을 제거하면 이진 표현에서는 항상 최상위 자릿수는 1이다("0"을 제외하고). 이 특성을 교묘하게 이용해 최상위 자릿수를 생략하는 표현 기법이 있으며, "케치 표현"이라고 불린다.
다음과 같은 기준은 특히 회계 데이터에 적용되며, 벤포드의 법칙이 적용될 것으로 예상된다.[69]
; 벤포드의 법칙을 따를 것으로 예상되는 분포
- 평균이 중앙값보다 크고 왜도가 양수인 경우
- 수의 수학적 결합으로 생성된 숫자: 예를 들어, 수량 × 가격
- 거래 수준 데이터: 예를 들어, 지출, 판매
; 벤포드의 법칙을 따르지 않을 것으로 예상되는 분포
- 숫자가 순차적으로 할당되는 경우: 예를 들어, 수표 번호, 송장 번호
- 인간의 사고에 의해 숫자가 영향을 받는 경우: 예를 들어, 심리적 임계값으로 설정된 가격 (9.99달러)
- 회사별 숫자가 많은 계정: 예를 들어, 100달러 환불을 기록하기 위해 설정된 계정
- 내장된 최소 또는 최대값을 가진 계정
- 수의 차수가 범위를 벗어나는 분포
연속된 자연수의 제곱근과 역수는 이 법칙을 따르지 않는다.[64] 유한 범위 내의 소수는 일반화된 벤포드의 법칙을 따르며, 범위의 크기가 무한대에 가까워질수록 균등 분포에 접근한다.[65] 지역 전화번호 목록은 벤포드의 법칙을 위반한다.[66] 1960년과 1970년 인구 조사에 따르면, 인구 2,500명 이상인 5개 미국 주의 모든 지역의 인구는 벤포드의 법칙을 위반했는데, 19%만이 숫자 1로 시작하고 20%는 숫자 2로 시작했기 때문이다. 이는 2,500에서 절단하면 통계적 편향이 발생하기 때문이다.[64] 병리 보고서의 마지막 숫자는 반올림으로 인해 벤포드의 법칙을 위반한다.[67]
여러 자릿수에 걸쳐 있지 않은 분포는 벤포드의 법칙을 따르지 않는다. 예를 들어 키, 몸무게, IQ 점수가 있다.[24][68]
5. 첫 번째 자릿수 이후의 일반화
어떤 숫자 집합에서 첫째 자리 숫자 ''d'' (''d'' ∈ {1, ..., 9})가 다음 확률 분포를 따를 때, 이 집합이 벤포드의 법칙을 따른다고 한다.[20]
:
이러한 숫자 집합에서 각 첫째 자리 숫자의 분포는 아래 표와 같다.
벤포드의 법칙은 첫째 자리 숫자를 넘어, 임의의 자릿수 ''n''으로 시작하는 숫자의 확률 분포로 확장될 수 있다.[71]
:
예를 들어, "314"로 시작하는 숫자를 만날 확률은 이다.
이 결과를 이용하면 특정 위치에서 특정 숫자가 나타날 확률을 계산할 수 있다. 예를 들어, 두 번째 자리에 "2"가 나타날 확률은 다음과 같다.[71]
:
일반적으로, ''d'' (''d'' = 0, 1, ..., 9)가 ''n''번째 (''n'' > 1) 숫자로 나타날 확률은 다음과 같다.
:
''n''이 증가함에 따라 ''n''번째 숫자의 분포는 각 숫자에 대해 10%의 균일 분포에 빠르게 수렴한다.[71] 4자릿수만 되어도 "0"은 10.0176%, "9"는 9.9824%로 나타나 균일 분포에 근접한다.
아래는 1, 2, 3번째 자리 숫자의 분포를 나타낸 표이다.
벤포드의 법칙은 십진법 외의 다른 기수법에도 적용될 수 있다.[9] 기수 ''b'' (''b'' ≥ 2)인 모든 기수에서 일반적인 형태는 다음과 같다.
:
1진법 및 2진법의 경우 벤포드의 법칙은 모든 수(0 또는 공집합 제외)가 1로 시작하므로 성립하지만, 자명하다. 그러나 두 번째 숫자 이후에는 이진법에서도 자명하지 않다.[10]
실제 벤포드의 법칙을 활용할 때는 두 번째 자릿수 이후도 함께 사용한다.[81]
6. 역사
벤포드의 법칙은 1881년 캐나다계 미국인 천문학자 사이먼 뉴컴이 처음 발견했다. 뉴컴은 로그 표에서 1로 시작하는 앞 페이지가 다른 페이지보다 훨씬 더 닳아 있다는 것을 발견했다.[11] 이는 뉴컴이 발표한 최초의 관찰 사례이며, 두 번째 숫자에 대한 분포도 포함하고 있다. 뉴컴은 숫자 ''N''이 숫자의 첫 번째 자릿수가 될 확률이 log(''N'' + 1) − log(''N'')과 같다는 법칙을 제안했다.
1938년 물리학자 프랭크 벤포드는 이 현상을 다시 언급하며,[7] 20개의 서로 다른 영역의 데이터를 사용하여 검증하고 공로를 인정받았다. 벤포드의 데이터 세트는 다음과 같다.
이 발견은 나중에 벤포드의 이름을 따서 명명되었으며, 이는 스티글러의 법칙의 한 예이다.
1995년, 테드 힐은 아래에 언급된 혼합 분포에 대한 결과를 증명했다.[25][12]
7. 통계적 검정
카이제곱 검정은 벤포드의 법칙 준수 여부를 검사하는 데 사용되었지만, 표본 크기가 작을 때는 통계적 검정력이 낮다.
콜모고로프-스미르노프 검정과 카이퍼 검정은 표본 크기가 작을 때, 특히 스티븐스의 보정 계수를 사용할 때 더 강력하다.[53] 이러한 검정은 이산 분포에 적용할 때 지나치게 보수적일 수 있다. Morrow는 벤포드 검정 값을 생성했다.[54] 검정 통계량의 임계값은 다음과 같다.
이러한 임계값은 주어진 유의 수준에서 벤포드의 법칙 준수 가설을 기각하는 데 필요한 최소 검정 통계량 값을 제공한다.
이 법칙에 특정한 두 가지 대안 검정이 발표되었다. 먼저, 최대 () 통계량[55]은 다음과 같다.
:
선행 계수 는 Leemis의 원래 공식에는 나타나지 않으며,[55] 이후 Morrow가 논문에서 추가했다.[54]
둘째, 거리 () 통계량[56]은 다음과 같다.
:
여기서 FSD는 첫 번째 유효 숫자이고, 은 표본 크기이다. Morrow는 이 두 통계량의 임계값을 결정했으며, 이는 다음과 같다.[54]
Morrow는 임의 변수 (연속 PDF)를 표준 편차 ()로 나눈 경우, 임의 변수 의 첫 번째 유효 숫자의 분포 확률이 벤포드의 법칙과 > 0보다 작게 다르게 되도록 하는 일부 값 를 찾을 수 있음을 보여주었다.[54] 의 값은 의 값과 임의 변수의 분포에 따라 달라진다.
부트스트래핑 및 회귀를 기반으로 하는 회계 사기 탐지 방법이 제안되었다.[57]
벤포드의 법칙과의 일치를 결론짓는 것이 목표라면, 위에서 언급한 적합도 검정은 부적절하다. 이 경우 특정 동등성 검정을 적용해야 한다. 경험적 분포는 확률 질량 함수 간의 거리(예: 총 변동 거리 또는 일반적인 유클리드 거리)가 충분히 작으면 벤포드의 법칙과 동등하다고 한다. 벤포드의 법칙에 적용하여 이러한 검사 방법은 Ostrovski에 설명되어 있다.[58]
8. 적용 범위
벤포드의 법칙은 여러 자릿수에 걸쳐있는 데이터에 가장 정확하게 적용되는 경향이 있다. 데이터가 더 많은 자릿수를 균등하게 포함할수록 벤포드의 법칙은 더 정확하게 적용된다. 예를 들어, 영국의 정착지 인구를 나타내는 숫자 목록에는 벤포드의 법칙이 적용될 수 있지만, 인구 300명에서 999명 사이의 마을로 정의된 "정착지"에는 적용되지 않는다.[13][14]
실제 데이터가 여러 자릿수에 걸쳐 비교적 균일하게 분포하는 경우(예: 주식 시장 가격, 마을 인구) 벤포드의 법칙을 매우 정확하게 만족시킬 가능성이 높다. 반면, 대부분 한 자릿수 내에 있는 분포(예: IQ 점수, 성인 키)는 벤포드의 법칙을 따르지 않을 가능성이 높다.[13][14]
벤포드의 법칙은 곱셈 변동에서 비롯되는 경우가 많다.[22] 예를 들어, 주가가 매일 무작위 요인으로 곱해지면 오랜 기간 동안 벤포드의 법칙을 만족하는 경향이 있다. 주가의 ''로그''가 확률보행을 겪으며, 중심 극한 정리에 따라 분포가 넓어지기 때문이다.[22] 반면 덧셈 변동은 정규 분포로 이어져 벤포드의 법칙을 만족하지 않는다.
안톤 포르만은 확률 변수의 긴 오른쪽 꼬리 분포가 뉴컴-벤포드의 법칙과 일치하며, 두 확률 변수의 비율 분포에서 적합성이 향상된다는 연구 결과를 제시했다.[23] IQ 점수나 인간 신장과 같은 정규 분포를 따르는 변량은 벤포드의 법칙을 따르지 않지만,[24] 여러 분포에서 숫자를 "혼합"하면 벤포드의 법칙이 다시 나타날 수 있다.[25][26]
길이 목록에서 첫 번째 숫자의 분포는 측정 단위(미터, 야드, 피트 등)에 관계없이 일반적으로 비슷할 수 있다. 이는 화폐 단위에도 적용된다. 그러나 성인 키와 같이 특정 범위로 제한되는 경우에는 단위에 따라 첫 번째 숫자의 분포가 달라질 수 있다. 데이터 집합의 첫 번째 숫자의 분포가 스케일 불변성을 가지면 벤포드의 법칙이 적용된다.[28][29]
몇몇 무한 정수 수열(피보나치 수,[59][60] 계승,[61] 2의 거듭제곱[62][63] 등)과 지수 성장 또는 지수 감소 과정은 벤포드의 법칙을 정확히 만족하는 것으로 증명되었다.
회계 데이터에 벤포드의 법칙을 적용할 때 고려해야 할 기준은 다음과 같다.[69]
수학적으로, 벤포드의 법칙은 테스트 중인 분포가 "벤포드의 법칙 적합성 정리"에 부합하는 경우, 즉 확률 밀도 함수의 로그의 푸리에 변환이 모든 정수 값에 대해 0일 경우 적용된다.
참조
[1]
논문
Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem
http://digitalcommon[...]
2011
[2]
웹사이트
Benford's Law
http://mathworld.wol[...]
2015-06-07
[3]
학술지
A Statistical Derivation of the Significant-Digit Law
https://projecteucli[...]
[4]
서적
Nonparametric Statistics with Applications to Science and Engineering
[5]
학술지
The mathematics of Benford's law: a primer
https://doi.org/10.1[...]
2020-06-30
[6]
학술지
The Surprising Accuracy of Benford's Law in Mathematics
https://doi.org/10.1[...]
2020-03-15
[7]
학술지
The law of anomalous numbers
1938-03
[8]
문서
They should strictly be bars but are shown as lines for clarity.
[9]
웹사이트
Benford's Law as a Logarithmic Transformation
http://www.maxwell-c[...]
2020-11-15
[10]
서적
Transformation Invariance of Benford Variables and their Numerical Modeling
Recent Researches in Automatic Control and Electronics
[11]
학술지
Note on the frequency of use of the different digits in natural numbers
[12]
학술지
Base-invariance implies Benford's law
[13]
서적
The Scientist and Engineer's Guide to Digital Signal Processing
http://www.dspguide.[...]
2012-12-15
[14]
학술지
A simple explanation of Benford's Law
https://www.stat.auc[...]
[15]
논문
Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem
http://digitalcommon[...]
2011
[16]
학술지
On entropy and generators of measure-preserving transformations
[17]
서적
Entropy in Dynamical Systems
https://books.google[...]
Cambridge University Press
2011-05-12
[18]
서적
Ergodic Theory, Entropy
Springer
[19]
학술지
Images and Benford's Law
[20]
서적
Benford's Law: Theory and Applications
https://books.google[...]
Princeton University Press
2015-06-09
[21]
학술지
Thermodynamics of Benford's first digit law
[22]
학술지
Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf
[23]
학술지
The Newcomb–Benford law in its relation to some common distributions
[24]
학술지
The Newcomb–Benford Law in Its Relation to Some Common Distributions
[25]
학술지
A Statistical Derivation of the Significant-Digit Law
http://digitalcommon[...]
[26]
학술지
The first digit phenomenon
http://people.math.g[...]
1998-07-08
[27]
학술지
From Uniform Distributions to Benford's Law
http://lmrs.univ-rou[...]
2015-08-13
[28]
학술지
On the Distribution of First Significant Digits
http://projecteuclid[...]
[29]
웹사이트
Benford's Law
https://mathworld.wo[...]
[30]
웹사이트
Benford's Law
https://wwwf.imperia[...]
2020-11-15
[31]
학술지
A basic theory of Benford's Law
https://projecteucli[...]
2011-06
[32]
학술지
Benford's Law (Letters to the Editor)
[33]
에피소드
From Benford to Erdös
https://www.wnycstud[...]
2009-09-30
[34]
논문
Election Forensics: Vote Counts and Benford’s Law
http://www-personal.[...]
2006-07-18
[35]
뉴스
Election forensics
https://www.economis[...]
The Economist
2007-02-22
[36]
논문
Benford's Law and the Detection of Election Fraud
https://www.cambridg[...]
2011
[37]
논문
Comment on "Benford's Law and the Detection of Election Fraud"
https://www.cambridg[...]
2011
[38]
뉴스
Statistics hint at fraud in Iranian election
https://www.newscien[...]
New Scientist
2009-06-24
[39]
문서
Note on the presidential election in Iran, June 2009
http://www-personal.[...]
University of Michigan
2009-06-29
[40]
논문
A first-digit anomaly in the 2009 Iranian presidential election
[41]
뉴스
The Devil Is in the Digits: Evidence That Iran's Election Was Rigged
https://www.washingt[...]
The Washington Post
2009-06-20
[42]
서적
Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection
Wiley
[43]
서적
Election Forensics: The Second-Digit Benford's Law Test and Recent American Presidential Elections
http://www-personal.[...]
Brookings Institution Press
[44]
논문
When Does the Second-Digit Benford's Law-Test Signal an Election Fraud? Facts or Misleading Test Results
2011
[45]
뉴스
Fact check: Deviation from Benford's Law does not prove election fraud
https://www.reuters.[...]
2020-11-10
[46]
웹사이트
Benford's law and the 2020 US presidential election: nothing out of the ordinary
https://physicsworld[...]
Physics World
2020-11-19
[47]
간행물
The promises and pitfalls of Benford's law
https://rss.onlineli[...]
Significance
2016-06
[48]
뉴스
The special trick that helps identify dodgy stats
https://www.theguard[...]
2011-09-16
[49]
논문
Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction
2005-12-01
[50]
논문
Genome sizes and the benford distribution
[51]
논문
Not the First Digit! Using Benford's Law to detect fraudulent scientific data
[52]
논문
Use of Benford's law on academic publishing networks
https://www.scienced[...]
2021-08-01
[53]
논문
Use of the Kolmogorov–Smirnov, Cramér–von Mises and related statistics without extensive tables
[54]
서적
Benford's Law, families of distributions and a test basis
http://cep.lse.ac.uk[...]
2014-08
[55]
논문
Survival distributions satisfying Benford's Law
[56]
논문
Breaking the (Benford) law: Statistical fraud detection in campaign finance
[57]
논문
An effective and efficient analytic technique: A bootstrap regression procedure and Benford's Law
[58]
논문
Testing equivalence of multinomial distributions
https://www.research[...]
2017-05
[59]
논문
Benford's Law for Fibonacci and Lucas Numbers
[60]
논문
An Application of Uniform Distribution to the Fibonacci Numbers
[61]
논문
An Observation on the Significant Digits of Binomial Coefficients and Factorials
[62]
문서
In general, the sequence k1, k2, k3, etc., satisfies Benford's law exactly, under the condition that log10 k is an irrational number. This is a straightforward consequence of the equidistribution theorem.
[63]
논문
The First Digit Problem
[64]
논문
The first digit problem
1976-08-09
[65]
웹사이트
New Pattern Found in Prime Numbers
https://phys.org/new[...]
[66]
논문
Breaking the (Benford) Law: Statistical Fraud Detection in Campaign Finance
https://www.jstor.or[...]
2007
[67]
논문
Terminal digit preference: beware of Benford's law
[68]
간행물
Understanding and Applying Benford’s Law
https://www.isaca.or[...]
ISACA Journal
2011-05-01
[69]
논문
The effective use of Benford's law to assist in detecting fraud in accounting data
[70]
논문
Explicit bounds for the approximation error in Benford's Law
[71]
논문
The Significant-Digit Phenomenon
http://digitalcommon[...]
[72]
웹사이트
Benford's Law: An empirical investigation and a novel explanation
http://dces.essex.ac[...]
Department of Computer Science, Univ. Essex
[73]
논문
A comparative analysis of the bootstrap versus traditional statistical procedures applied to digital analysis based on Benford's law
http://www.bus.lsu.e[...]
2012-06-30
[74]
논문
The law of anomalous numbers
http://links.jstor.o[...]
[75]
논문
Note on the frequency of use of the different digits in natural numbers
[76]
문서
대수 스케일에서의 확률 분포
[77]
논문
A simple explanation of Benford's Law
https://doi.org/10.1[...]
[78]
논문
The first digit phenomenon
http://www.tphill.ne[...]
[79]
논문
A statistical derivation of the significant-digit law
http://www.tphill.ne[...]
[80]
논문
Benford's law
[81]
논문
I've Got Your Number
http://www.aicpa.org[...]
[82]
논문
The Significant-Digit Phenomenon
http://www.jstor.org[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com




